请注意,本文编写于 44 天前,最后修改于 44 天前,其中某些信息可能已经过时。
目录
Problem: 1411. 给 N x 3 网格图涂色的方案数
1. 有向图路径数量
在这个问题中,我们可以将网格图的每一行都可以抽象成一个顶点(vertex),我们可以将这个问题抽象成:
有向图G(V,E)
- V代表顶点集,
- E代表边集,其中的每个元素代表{from_state,to_state},from_state的下一行可以是to_state 如下图所示:
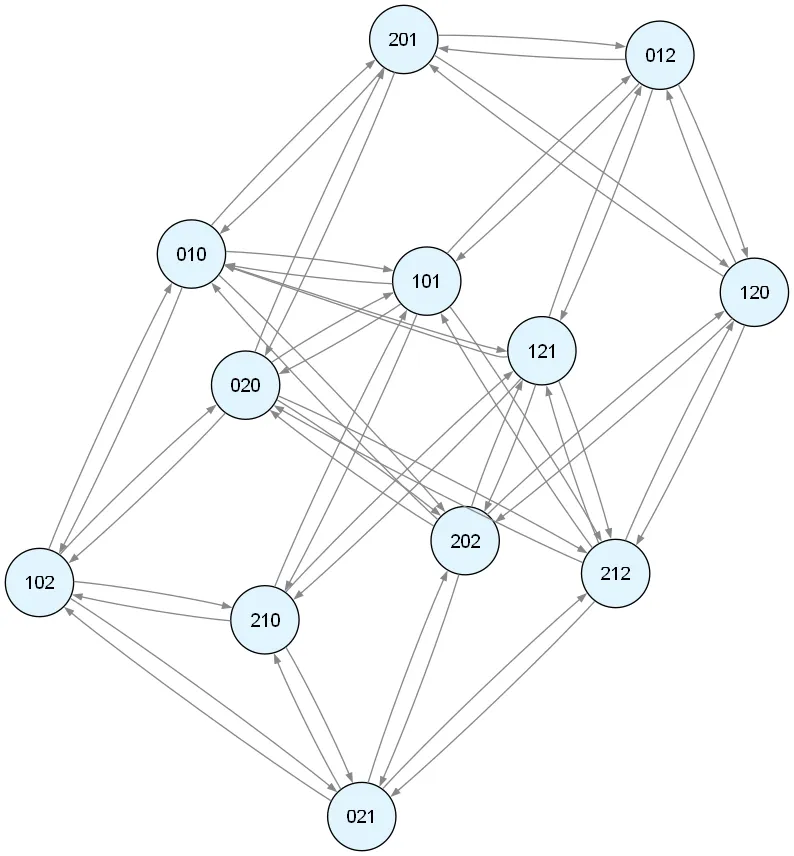
我们要求的就是: 从这个图中的每个点出发,能够走出多少条长度为n - 1的路径
Code
cpp
#include <vector>
#include <ranges>
#include <algorithm>
#include <print>
using namespace std;
class Solution {
private:
static bool check_state(int state){
int left = (state / 9) % 3;
int mid = (state / 3) % 3;
int right = (state) % 3;
if((left == mid) or (right == mid)){
return false;
}
return true;
}
static bool check_edge(int first_state,int second_state){
int first_color[3] = {(first_state / 9) % 3,(first_state/ 3) % 3,(first_state) % 3 };
int second_color[3] = {(second_state / 9) % 3,(second_state/ 3) % 3,(second_state) % 3 };
for(int i = 0;i < 3;i++){
if(first_color[i] == second_color[i]){
return false;
}
}
return true;
}
public:
using ll = long long;
static constexpr ll mod = 1'000'000'007;
int numOfWays(int n) {
vector<vector<int>> state_transition_table(27);
int cnt = 0;
for(int first_state = 0; first_state < 27;first_state++){
if(check_state(first_state) == false){
continue;
}
for(int second_state = 0;second_state < 27;second_state++){
if(check_state(second_state) == false){
continue;
}
if(check_edge(first_state,second_state)){
state_transition_table[first_state].emplace_back(second_state);
}
}
}
vector<int> state_sum = state_transition_table |
views::transform([](vector<int>& v){ return int{!v.empty()};})|
ranges::to<vector<int>>();
for(int step = 0;step < n - 1;step++){
vector<int> pre_state_sum = state_sum;
for(int from_state = 0;from_state < 27;from_state++){
state_sum[from_state] = 0;
for(int to_state : state_transition_table[from_state]){
state_sum[from_state] = (state_sum[from_state] + pre_state_sum[to_state] * 1LL) % mod;
}
}
}
return ranges::fold_left(state_sum,0,[&](int lhs,int rhs){ return (lhs + rhs) % mod;});
}
};
复杂度
- 时间复杂度: O(n∗27)
- 空间复杂度: O(n∗5)
2. 顶点聚合
实际上,我们不需要这么多顶点,具体来说,我们可以看到顶点一共有两种模式,即ABA模式和ABC模式。
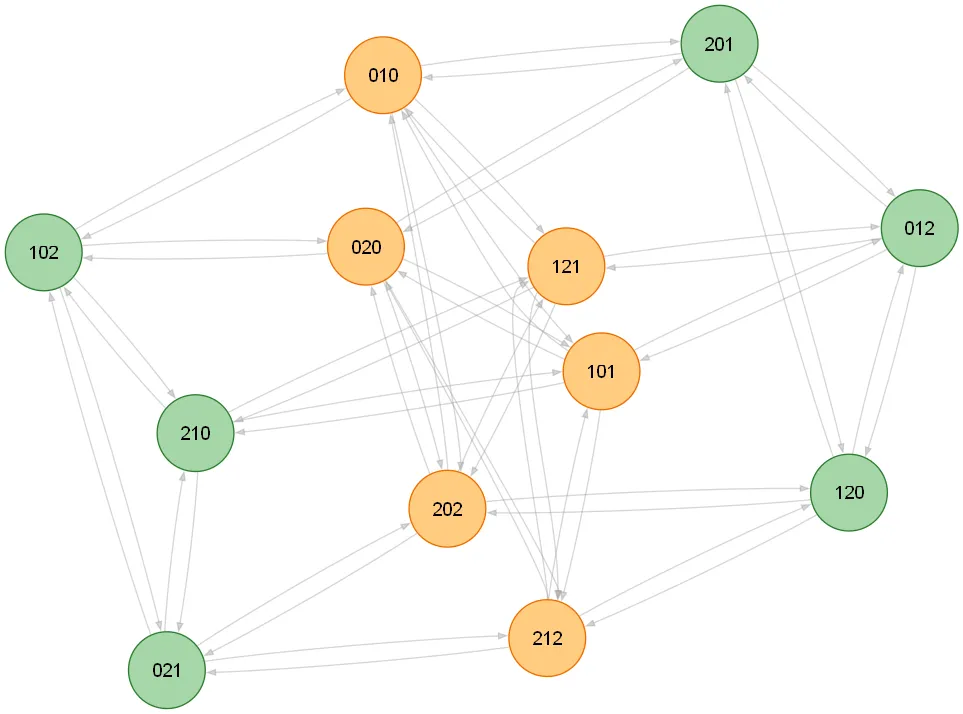
进一步,我们对图进行收缩,有:
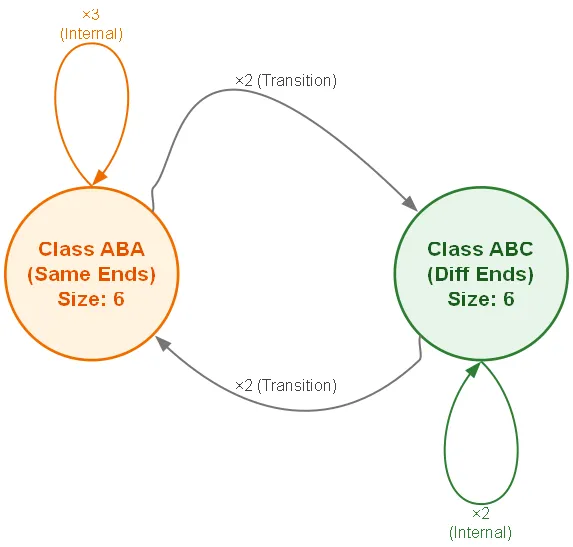
公式
原先需要对12个点进行求值,现在只需要对2个pattern进行求值。
公式为:
- state[n][ABA] = 3 * state[n - 1][ABA] + 2 * state[n - 1][ABC]
- state[n][ABC] = 2 * state[n - 1][ABA] + 2 * state[n - 1][ABC]
其中 state[1][ABC] = 6 state[1][ABA] = 6
模板元优化
由于本题n的数量较小,且相同的输入,永远会产生相同的结果,所以,可以在编译期就计算完成
Code
C++#include <vector>
#include <ranges>
#include <algorithm>
#include <print>
using namespace std;
using ll = long long;
inline static constexpr ll mod = 1'000'000'007;
struct TableData {
int status[5002];
};
inline static consteval TableData init_tables() {
TableData data = {};
data.status[1] = 12;
data.status[2] = 54;
for (int i = 3; i <= 5000; ++i) {
data.status[i] = (7 * mod + 5LL * data.status[i - 1] - 2LL * data.status[i - 2]) % mod;
}
return data;
}
class Solution {
public:
static constexpr TableData cache = init_tables();
int numOfWays(int n) {
// state[n][ABA] = 3 * state[n - 1][ABA] + 2 * state[n - 1][ABC]
// state[n][ABC] = 2 * state[n - 1][ABA] + 2 * state[n - 1][ABC]
return cache.status[n];
}
};
复杂度
- 时间复杂度: O(1)
- 空间复杂度: O(1)
本文作者:barrenham
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
目录